문제
https://www.acmicpc.net/problem/12015
12015번: 가장 긴 증가하는 부분 수열 2
첫째 줄에 수열 A의 크기 N (1 ≤ N ≤ 1,000,000)이 주어진다. 둘째 줄에는 수열 A를 이루고 있는 Ai가 주어진다. (1 ≤ Ai ≤ 1,000,000)
www.acmicpc.net
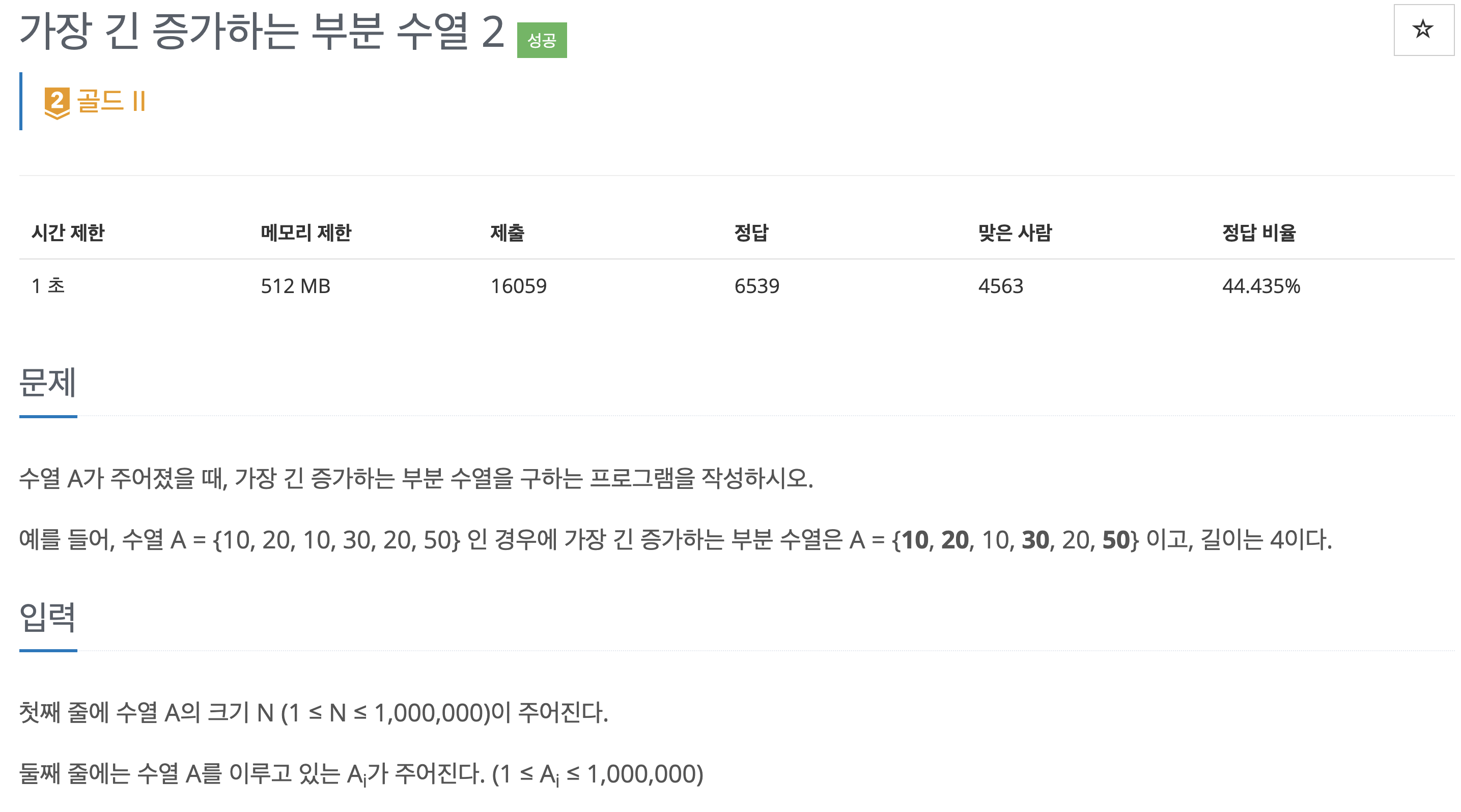
해당 문제는 Longest Increasing Subsequence(LIS), 최장증가부분수열 문제로
수열의 크기가 1,000,000개로 주어지기 때문에 O(n^2)의 시간복잡도의 알고리즘은 시간초과가 난다.
이분탐색을 활용하여 풀어야하는 문제이다.
다음과 같은 풀이를 이용하였다.
else 구문을 보면 입력받은 num 값을 다시 갱신해주고있다.
이 부분이 이문제의 핵심이 아닐까 생각한다.
왜그런지 살펴보자면,
만약 A = [ 5, 15, 35, 30, 25, 60, 40, 100] 이라는 수열이 있다고 해보자. 해당 수열의
그러면 Vector v 에는 다음과 같이 추가와 데이터 갱신이 반복되면서 최장증가수열의 개수가 구해지게된다.
| i = 0 | NUM = 5 | V = { 5 } | V.Size = 1 로 증가 |
| i = 1 | NUM = 15 | V = { 5 , 15 } | V.Size = 2 로 증가 |
| i = 2 | NUM = 35 | V = { 5, 15, 35 } | V.Size = 3 으로 증가 |
| i = 3 | NUM = 30 | V = { 5, 15, 30 } | V.Size = 3 유지, V[2] 값 35-> 30으로 갱신 |
| i = 4 | NUM = 25 | V = { 5, 15, 25 } | V.Size = 3 유지, V[2] 값 30-> 25으로 갱신 |
| i = 5 | NUM = 60 | V = { 5, 15, 25, 60 } | V.Size = 4 로 증가 |
| i = 6 | NUM = 40 | V = { 5, 15, 25, 40 } | V.Size = 4 유지, V[3] 값 60-> 40으로 갱신 |
| i = 7 | NUM = 100 | V = { 5, 15, 25, 40, 100 } | V.Size = 5 로 증가 |
만약
벡터마지막 원소보다 작은 값이 추가되었을때 작은값으로 갱신해주지않는다면
최장증가수열이 구해지지 않고, 5 15 35 60 100 와 같이 들어오는 순서대로 가장 큰 수열이 구해질 것이다.
코드
#include <iostream>
#include <vector>
using namespace std;
int n;
vector<int> v;
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
cin >> n;
for(int i = 0; i < n; i++) {
int num;
cin >> num;
auto it = lower_bound(v.begin(), v.end(), num);
if(it == v.end()) {
v.push_back(num);
} else {
*it = num;
}
}
cout << v.size() << "\n";
return 0;
}'개발 > 알고리즘' 카테고리의 다른 글
| 백준 14891 톱니바퀴 (0) | 2021.06.24 |
|---|---|
| 백준 14499 주사위 굴리기 (0) | 2021.06.22 |
| 분할 정복이란(Divide & Conquer) (0) | 2021.06.21 |
| 백준 1520 내리막 길 java (0) | 2021.06.20 |
| 백준 구간 나누기2 13397 (0) | 2021.06.18 |

